1~4. AI Math

AI를 위한 기본 수학 정리

1. Vector
벡터란 공간에서의 한 점을 나타내며 원점으로부터 상대적인 위치를 표현한다. 벡터에는 덧셈, 뺄셈, 스칼라곱 등의 연산이 가능하다. 
벡터의 norm은 원점에서부터의 거리를 의미하며 L1, L2-norm 등이 존재한다. Norm의 종류에 따라 기하학적인 성질이 달라진다.

• L1-Norm: 벡터의 각 원소들의 절대값의 합
• L2-Norm: Euclidean Distance

벡터 사이의 각
제 2 코사인 법칙을 이용하여 두 벡터 사이의 각도를 계산할 수 있다.

제2 코사인 법칙

내적을 이용하여 계산을 더 쉽게 할 수 있다. 두 벡터 x, y가 있다면 x, y의 내적은 x를 y에 정사영한 길이를 ||y||만큼 조정한 것이다. 
내적을 이용하여 두 벡터간의 유사도 를 계산할 수 있다.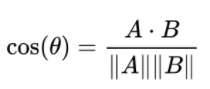

2. Matrix
행렬은 벡터를 원소로 가지는 2차원 배열. 1) 행렬을 공간상의 여러 점들의 집합, 즉 데이터의 모임으로 생각할 수 있다. 
2) 행렬은 벡터 공간에서 사용되는 연산자로 이해할 수도 있다. 

 

• 인덱스는 항상 행, 열 순으로 표기.
• 행렬곱을 통해 패턴을 추출할수 있고(Spectral clustering), 데이터를 압축할 수도 있다(PCA)
• 행렬의 내적은 numpy.inner()로 계산할 수 있으며 같은 행끼리의 내적을 계산. 

 

유사 역행렬
유사 역행렬(Pseudo-Inverse) 또는 무어 펜로즈(Moore-Penrose) 역행렬을 이용하여 (n, m) (n !=m ) 차원의 행렬의 역행렬을 구할 수 있다. numpy의 np.linagl.pinv() 함수를 이용하여 이를 구할 수 있다.

유사역행렬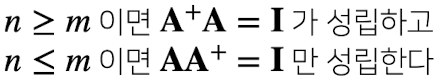

주의할 점

이를 이용하여 연립방정식의 해, 선형회귀식을 찾을 수 있다. 

3. Gradient Descent

미분을 이용하여 함수의 접선의 기울기를 구해서 함수의 증가/감소 방향을 알아내서 함수의 극대/극소점을 찾는다. 변수가 벡터이면 편미분을 이용하여 함수가 감소하는 방향을 알아내어, norm을 계산하여 종료조건을 설정한다.

 

SGD(확률적 경사하강법)를 이용하여 전체 batch가 아닌 일부를 사용하여 그레디언트 벡터를 계산하여 더 효율적으로 학습을 할 수 있다.

---

PEER SESSION

 

Q. 경사하강법으로 선형회귀 계수 구하는 방법?

유도과정

---

느낀점

처음이라 모든게 어색했지만, 열심히 해야겠다. 강의를 조금 더 꼼꼼히 봐서 수식적인 이해를 더 할 필요도 있는 것 같다.