8. 베이즈 통계학

조건부 확률: $ P(A|B) = P(A \cap B) / P(B) $ 로 사건 B가 일어났을 때 A가 발생할 확률

베이즈 정리: A라는 새로운 정보가 주어졌을 때 $ P(B) $로부터 $ P(B|A) $를 계산하는 방법 

정밀도 (Precision) : $ P(\theta|D) = TP / (TP + FP) $

베이즈 정리를 이용하여 새로운 데이터가 들어왔을 때 정밀도 뿐만아니라 갱신된 사후확률도 계산할 수 있다.

 

어떤 질병에 걸릴 확률이 0.1프로, 걸렸을 때 검진될 확률이 99%, 걸리지 않았을 때 오검진 될 확률이 10%라고 하면 질병에 걸렸다고 검진결과가 나왔을 때 정말로 감염될 확률은 아래와 같다.

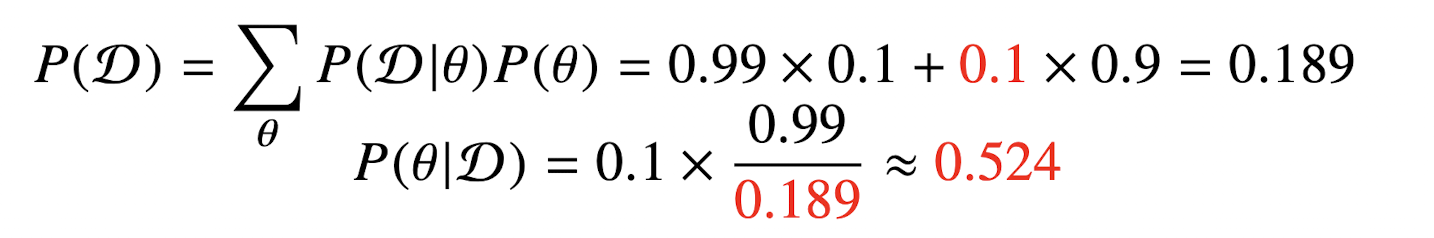
만약 검사를 한번 더 진행하여 사후확률을 갱신한다면 다음과 같이 계산된다. 

주의할점: 인과관계를 추론할 때 조건부 확률을 남용하면 안된다. 인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요하다.

인과관계에 관해 상당히 흥미로운 내용이 있었다. 위의 예제에서 전체적인 완치율을 조건부 확률로 보면 치료법 b가 더 높다. 하지만 작은 신장결석과 큰 신장결석의 완치율을 따로 볼 경우 치료방법 a의 완치율이 두 경우 모두에서 높은 것을 확인할 수 있다. 이는 Simpson's Paradox라고 불리는 대표적인 통계적 역설의 예시이다.

https://en.wikipedia.org/wiki/Simpson%27s_paradox

Simpson's paradox - Wikipedia

이 역설 문제를 해결하기 위해서는 신장결석 크기에 따른 인과관계에 따른 조정효과를 제거해줄 필요가 있다. 이는 모든 환자가 신장결석의 크기에 상관없이 하나의 치료법을 선택했다고 가정하여 z의 개입을 없애는 방식이다. 

조정효과를 제거했을 때 a의 완치율

조정효과를 제거했을 때 b의 완치율

위와 같은 통계적 역설에 대해 공부할 때 보면 좋은책이라고 한다.

https://www.amazon.com/Book-Why-Science-Cause-Effect/dp/046509760X

The Book of Why: The New Science of Cause and Effect: Pearl, Judea, Mackenzie, Dana: 9780465097609: Amazon.com: Books

---

피어세션 및 과제

아직 초반이라 질문이 많지 않아서 팀원들과 함께 강의/과제 정리를 어떻게 하는지 서로 공유하는 시간을 가졌고, 팀원들의 관심 분야에 대해 얘기해서 더 친해졌다.

---

느낀점

심슨의 역설의 상당히 흥미로웠고, 오류를 범하지 않기 위해 통계적 지식이 필요한 것을 느꼈다.  베이즈 정리에 대해서는 통계수업과 데이터마이닝 수업을 들으면서 많이 공부를 했음에도 불구하고 봐도봐도 헷갈리는 것 같다.