7. 통계 기본

통계적 모델링은 적절한 가정 위에서 확률분포를 추정하는 것이 목표이며, 유한한 개수의 데이터를 관찰하여 모집단의 분포를 근사적으로 추정한다. 

 

• 모수적 방법론(parametric): 데이터가 특정 확률분포를 따른다고 선험적으로(apriori) 가정한 후 그 분포를 결정
• 비모수적 방법론(non-parametric): 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 바뀜 -> 기계학습의 많이 사용, 비모수적 방법론이라고 모수가 없는것은 아니다.

확률분포 예시

• 데이터가 2개의 값(0 또는 1)만 가지는 경우 → 베르누이분포
• 데이터가 n개의 이산적인 값을 가지는 경우 → 카테고리분포
• 데이터가 [0,1] 사이에서 값을 가지는 경우 → 베타분포
• 데이터가 0 이상의 값을 가지는 경우 → 감마분포, 로그정규분포 등
• 데이터가 R 전체에서 값을 가지는 경우 → 정규분포, 라플라스분포 등

확률분포를 가정할때, 데이터를 생성하는 원리를 고려해야 하며, 모수를 추정한 후 통계적 검정을 이용하여 적절한 예측인지 검정해보는 것이 중요하다. 

 

표집분포(sampling distribution): 통계랑, 즉 표본이 아닌, 표본평균과 표본분산의 확률분포. sample distribution과 다르다.  N이 커질수록 정규분포를 따른다(중심극한정리). 예시로 아래 그림에서 베르누이 확률분포를 따르는 확률 변수들의 분포를 그려보면, 데이터가 적을때는 표본평균이 양 극단에 위치했는데, 데이터의 양이 증가함에 따라 표본평균의 확률분포가 정규분포의 모양을 따르고, N이 커짐에 따라 분산이 점점 작아지는 것을 확인할 수 있다. 

베르누이 분포의 표본분포 (출저: Daniel Resende)

최대가능도 추정법: 확률 분포마다 사용하는 모수가 다르기 때문에 적절한 통계량이 달라지게 되고, 최대가능도 추정법(maximum likelihood estimation, MLE)를 이용하여 이론적으로 가장 가능성이 높은 모수를 추정할 수 있다. 

$ argmax  $ : 함수 $ L(\theta; x) $ 를 최대로 만들기 위한 $ \theta $ 값을 찾는다

가능도 함수는 $ L(\theta; x) $ 이며, 모수 $ \theta $가 주어져 있을 때 x에 대한 함수로 나타내는 확률밀도/질량 함수와 다르게, 주어진 데이터 x에 대해 모수 $ \theta $ 를 변수로 둔 함수. 즉 모수 $ \theta $를 따르는 분포가 데이터 x를 관찰할 가능성!

• 가능도는 확률로 해석하면 안된다. $ \theta $에 대해 적분이나 모두 더해줬을 때 1이되는 것이 아니기 때문.
• 가능도는 대소비교를 가능하게 해준다.
• 데이터가 독립적으로 추출된 경우, 확률함수들의 곱으로 가능도 함수를 나타낼 수 있고, 양변에 로그를 씌운 로그 가능도를 이용하여 로그 가능도를 최적화하면 된다.

로그 가능도

로그 가능도를 사용하는 이유는 데이터의 숫자가 많은 경우 컴퓨터로 계산이 가능하게 해주기 위함이며, 경사하강법을 이용할 때 연산랑을 $ O(n^2) $ 에서 $ O(n) $ 으로 줄일 수 있다.

https://math.stackexchange.com/questions/892832/why-we-consider-log-likelihood-instead-of-likelihood-in-gaussian-distribution

Why we consider log likelihood instead of Likelihood in Gaussian Distribution

정규분포의 모수를 추정하는 경우 아래 식을 

평균과 분산에 대해 미분하여 미분값이 0이되는 평균값과 분산값을 찾으면 가능도를 최대화 할 수 있다. 

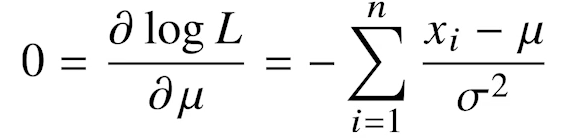
계산된 모수는 아래와 같다. 

https://angeloyeo.github.io/2020/07/17/MLE.html

최대우도법(MLE) - 공돌이의 수학정리노트

위 링크의 내용을 보면 더 이해를 잘 할 수 있었다. 

---

딥러닝에서도 최대 가능도 추정법을 이용하여 기계학습 모델을 학습시킬 수 있다. 

• 딥러닝 모델의 가중치를  𝜃=(𝐖(1),…,𝐖(𝐿)) 라고 했을 때 분류 문제에서 소프트맥스 벡터는 카테고리분포의 모수를 모델링
• 원핫벡터로 표현한 정답레이블 y를 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화할 수 있다.

기계학습의 사용되는 손실함수들은 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도된다. 

• 총 변동 거리 (Total Variation Distance, TV)
• 쿨백-라이블러 발산(Kullback-Leibler Divergence, KL)

쿨백 라이블러를 위와 같이 분해하면 앞의 term은 크로스 엔트로피, 뒤의 term은 엔트로피이고, 분류 문제에서 정답레이블을 P, 모델 예측을 Q라고 하면 최대가능도 추정법은 쿨백 라이블러 발산을 최소화 하는 것과 같아진다. 

[참고자료] https://3months.tistory.com/436

• 바슈타인 거리 (Wasserstein Distance) 

  ---

과제

• 다른 분포의 최대가능도 추정법

https://datascienceschool.net/02%20mathematics/09.02%20%EC%B5%9C%EB%8C%80%EA%B0%80%EB%8A%A5%EB%8F%84%20%EC%B6%94%EC%A0%95%EB%B2%95.html

9.2 최대가능도 추정법 — 데이터 사이언스 스쿨

• 분포에 따라 가능도함수와 확률밀도함수가 다른 것이 일반적이다.

---

1. 확률과 가능도의 차이는 무엇일까요? (개념적인 차이, 수식에서의 차이, 확률밀도함수에서의 차이)

• 확률: 어떤 시행에서 특정 결과가 나올 가능성. 시행 전 모든 경우의 수의 가능성은 정해져 있으며 그 총합은 1이다.
• 어떤 시행을 충분히 수행한 뒤, 그 결과를 토대로 경우의 수의 가능성을 도출. 가능성의 합이 1이 되지 않을 수 있다.

2. 확률 대신 가능도를 사용하였을 때의 이점은 어떤 것이 있을까요?

연속확률 분포에서는 구간이 아닌 이상 확률을 구하기 어려운데, 가능도는 연속확률분포에서도 구할 수 있어서 특정 사건의 확률을 구해 비교가 가능하다. 

 

3. 다음의 code snippet은 어떤 확률분포를 나타내는 것일까요? 해당 확률분포에서 변수 theta가 의미할 수 있는 것은 무엇이 있을까요?